Background
Recently, I decided to better understand database internals after coming across the storage chapter in Designing Data-Intensive Applications and what better way to learn than to build my own storage engine (a simple embedded LSM tree based Key Value store) that no one will ever use! Anyway, I’ll probably share more on the broader design as I near completion but for now, I want to focus on something that’s made a difference in speeding up reads.
A key characteristic of Log Structured Merge (LSM) tree based databases is that data is never updated in place. Instead, every write simply appends a new record to an ever growing log. Updates are simply writes of new values to existing keys while deletes are writes with an empty value and a tombstone to mark keys as removed (like a lazy delete).
The engine manages data through two layers : An in-memory store and a persistent component on disk. Reads and Writes first go to an in-memory buffer called Memtable. If the key cannot be found in the active memtable, several temporary read only memtables are checked before going to disk.
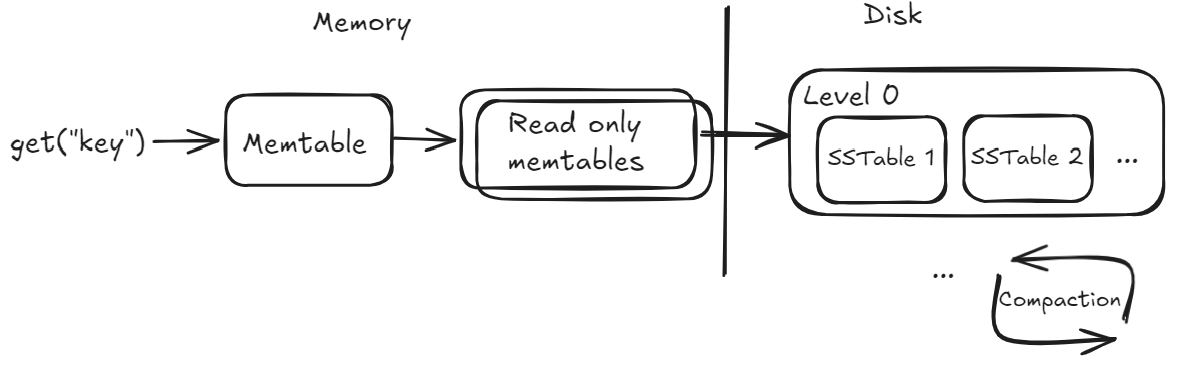 When the Memtable reaches its size threshold, its contents are sorted lexicographically based on keys and flushed to disk as ordered, immutable files called Sorted String Tables (SSTables).
As the size grows, the SSTables undergo a compaction process which merges multiple SSTables (more on this in a future blog post) while removing outdated key versions and deleted keys.
This design allows for fast sequential writes but slower reads over time as the engine may need to search through multiple SSTables to find the most recent value for a given search key, only to find out in the end that the key doesn’t exist. To speed this up, each SSTable includes metadata like the first and last key (aka. fence pointers). So if you’re looking for a key and it doesn’t fall within an SSTable’s start and end key range, you can skip searching that file entirely.
When the Memtable reaches its size threshold, its contents are sorted lexicographically based on keys and flushed to disk as ordered, immutable files called Sorted String Tables (SSTables).
As the size grows, the SSTables undergo a compaction process which merges multiple SSTables (more on this in a future blog post) while removing outdated key versions and deleted keys.
This design allows for fast sequential writes but slower reads over time as the engine may need to search through multiple SSTables to find the most recent value for a given search key, only to find out in the end that the key doesn’t exist. To speed this up, each SSTable includes metadata like the first and last key (aka. fence pointers). So if you’re looking for a key and it doesn’t fall within an SSTable’s start and end key range, you can skip searching that file entirely.
However, just knowing the key range isn’t enough to guarantee that a valid key exists/doesn’t exist in a given SSTable.
Bloom filters: What? How? Why?
Bloom filters are probabilistic data structures used to test set membership and are essentially just a sequence of bits. They help answer one big question: “Is this item not in the set?”. Unlike other data structures, they don’t store any actual data which makes them highly space-efficient even as the number of items increases.

Here’s how they work:
- During insertion, each key is hashed using multiple hash functions and each hash provides a position in a fixed-size bit array which are then set to 1.
- Whenever the existence of a key needs to be verified, the bits resulting from the hashes of the key are checked. If all the bits at those positions are 1, the key might be in the set but even if one bit is 0, the key is definitely not in the set.
Storing the bloom filters in memory can reduce unnecessary disk I/O by avoiding searches though SSTables in which the key is definitely not present in.
Here’s a little simulator for you to try out its behavior by inserting keys and checking for their presence. For the sake of demonstration each of the k hash functions cycle through sha256, sha1 and sha512 hashing algorithms. Adjust the bit count and hash functions to see how they influence the filter’s accuracy.
Tuning Bloom filters for SSTables
You might’ve noticed from the simulator above that there’s a tradeoff between the number of hash functions and the number of bits in the filter. Too few bits mean the filter fills up quickly, leading to higher false positive rates and while increasing the number of bits reduces the likelihood of false positive, it comes at the cost of more memory usage. I’ll spare you the math since I’m not very good at it myself instead if you’re very curious check this out.
To determine the optimal number of bits for the bloom filter based on the total number of entries in the SSTable and a desired false positive rate, we can use the following functions
// Calculate the size of the Bloom filter in bits
func bitsPerKey(entries int, falsePositiveRate float64) int {
size := -1.0 * float64(entries) * math.Log(falsePositiveRate) / math.Pow(math.Ln2, 2)
// Calculate the number of bits per key, rounding up
bitsPerKey := math.Ceil(size / float64(entries))
return int(bitsPerKey)
}
// Calculate the optimal number of hash functions (k).
func calculateHashFunctions(bitsPerKey, numKeys int) int {
// k = (totalBits / entries) * ln(2)
return int(math.Ceil(float64(bitsPerKey) * math.Ln2))
}For example, calling bitsPerKey(10000,0.01) would return the number of bits per key needed to achieve a 1% false positive rate for 10,000 entries.
Double Hashing
Calculating mutiple hash functions for every key lookup can become computationally expensive. This is where double hashing, a technique introduced in Less Hashing, Same Performance: Building a Better Bloom Filter (Kirsch & Mitzenmacher, 2006) can help.
Here, double hashing would use 2 hash functions to achieve similar results but instead of generating k independent hashes for each element, it modifies the first hash using the second hash k times to spread out the positions in the bit array and reduce collisions without extra expensive hash calculations.
func (bf *BloomFilter) MayContain(key []byte) bool {
totalBits := len(bf.filter)*8
hash:= preferredHashFunction(key)
hash2 := preferredHashFunction2(key)
for i := 0; i < bf.k; i++ {
// Calculate bit position using hash value modulo bit array length
bitPosition := hash % uint32(totalBits)
// Check if the bit is set in the filter
if !bf.getBit(int(bitPosition)) {
return false
}
// Update hash value with double hashing
hash = hash + hash2
}
return true
}Once the filter is created, here’s how it fits into the key search.
func shouldSearchTable(key []byte, sst *SSTable) bool {
// Fence pointer check: Key within first and last keys of the SSTable
if bytes.Compare(key, sst.GetFirstKey()) >= 0 && bytes.Compare(key, sst.GetLastKey()) <= 0 {
// Bloom filter check
if sst.BloomFilter.MayContain(key) {
// key is potentially in the table, continue with search
return true
}
return false
}
return false // key not within SSTable range
}It’s Benchmarkin’ Time!
To understand how much of a difference Bloom filters can make, I ran a simple benchmark on my storage engine setup. The idea was to simulate a moderately heavy workload: 1 million writes (with 16-byte keys and 64-byte values), followed by 500K reads. I disabled the WAL to isolate read and write path effects without durability noise, and compactions are out of the picture as they haven’t been implemented yet..
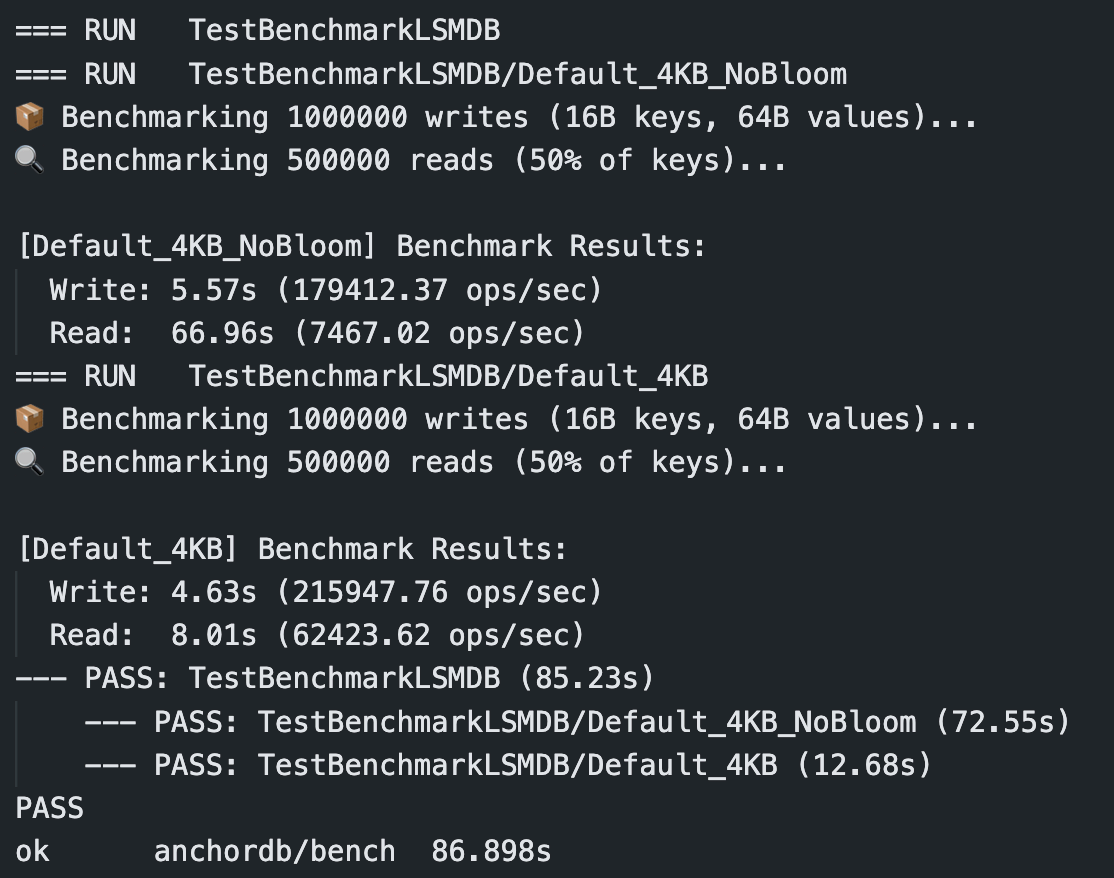
Write performance was roughly comparable with and without Bloom filters, as expected since writes don’t perform key lookups. The real win, however, was in read performance with nearly an 8x boost.